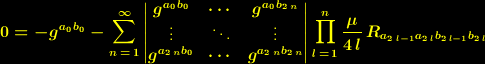
| Home | Relativistische Vielweltentheorie |
| Beispiel: Einbeziehung nichtmetrischer Größen | Lovelock-Tensoren |
| Einige Variationsergebnisse | Sonstiges |
| vielweltentheorie.pdf | relativistische@vielweltentheorie.de |
Die hier angegebenen Lösungen beziehen sich auf die Feldgleichung:
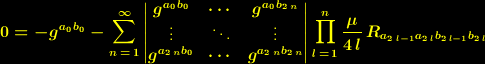 | (1) |
Für 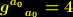 ist das Linienelement
ist das Linienelement
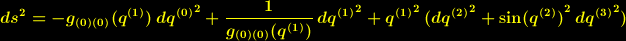 | (2) |
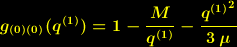 | (3) |
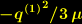 eine Lösung der Feldgleichung (1). Die Schwarzschildmetrik hat bei
eine Lösung der Feldgleichung (1). Die Schwarzschildmetrik hat bei 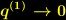 eine Singularität, die sich nicht durch Koordinatentransformationen beseitigen lässt.
eine Singularität, die sich nicht durch Koordinatentransformationen beseitigen lässt.
Die für 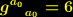 gültige Lösung
gültige Lösung
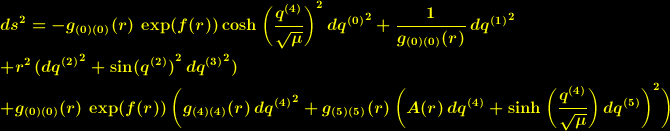 | (4) |
mit:
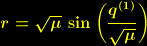 | (5) |
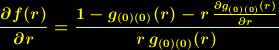 | (6) |
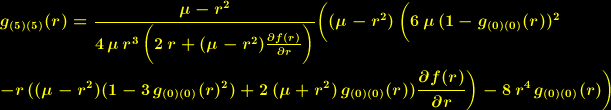 | (7) |
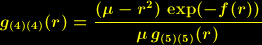 | (8) |
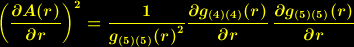 | (9) |
und:
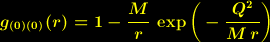 | (10) |
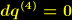 ,
, 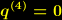 ,
, 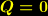 und
und  als Grenzfall und erlaubt für
als Grenzfall und erlaubt für  singularitätsfreie Lösungen, die im Bereich für
singularitätsfreie Lösungen, die im Bereich für  mit
mit 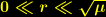 durch die Schwarzschildlösung näherungsweise beschrieben werden kann.
Aus dem Grenzfall für
durch die Schwarzschildlösung näherungsweise beschrieben werden kann.
Aus dem Grenzfall für  ergibt sich daraus die Lösung:
ergibt sich daraus die Lösung:
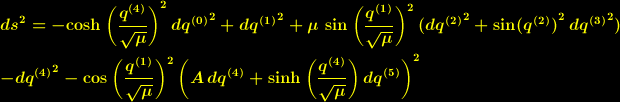 | (11) |
 und
und 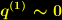 als Näherung für (4). Der Teilbeireich dieser Lösung, der durch
als Näherung für (4). Der Teilbeireich dieser Lösung, der durch
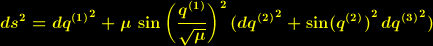 | (12) |
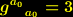 . Diese Lösung stellt eine dreidimensionale Kugeloberfläche mit dem Radius
. Diese Lösung stellt eine dreidimensionale Kugeloberfläche mit dem Radius 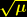 dar.
dar.
| Home | Relativistische Vielweltentheorie |
| Beispiel: Einbeziehung nichtmetrischer Größen | Lovelock-Tensoren |
| Einige Variationsergebnisse | Sonstiges |
| vielweltentheorie.pdf | relativistische@vielweltentheorie.de |
| © 2005-2008 Thorsten Krechel. Alle Rechte vorbehalten. |