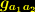
Der metrische Tensor ergibt sich aus der Variation der invarianten Wirkung:
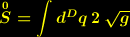 | (1) |
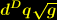 stellt hier das invariante Volumenelement eines
stellt hier das invariante Volumenelement eines 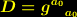 -dimensionalen Raumes dar, in der
-dimensionalen Raumes dar, in der 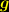 die Determinante des metrischen Tensors bedeutet. Die Komponenten des metrischen Tensors
die Determinante des metrischen Tensors bedeutet. Die Komponenten des metrischen Tensors 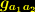 stellen die Feldvariablen dar, nach denen variiert wird. Als Variationsergebnis ergibt sich dann aus
stellen die Feldvariablen dar, nach denen variiert wird. Als Variationsergebnis ergibt sich dann aus 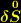 , indem alle auftretenden Variationen durch
, indem alle auftretenden Variationen durch 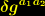 ausgedrückt werden:
ausgedrückt werden:
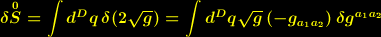 | (2) |
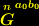 , die den Krümmungstensor
, die den Krümmungstensor
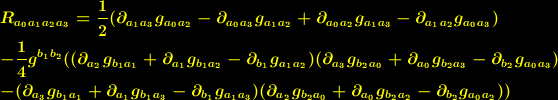 | (3) |
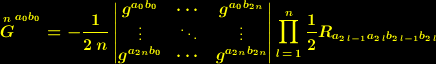 | (4) |
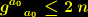 . Für
. Für 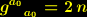 gibt es dabei noch eine besondere Beziehung zwischen den Skalaren
gibt es dabei noch eine besondere Beziehung zwischen den Skalaren
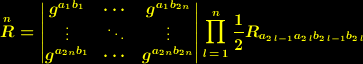 | (5) |
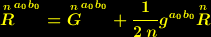 | (6), |
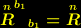 | (7) |
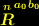 verschwinden für
verschwinden für 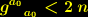 , und es gilt:
, und es gilt:
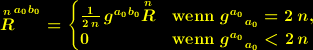 | (8) |
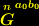 (4) ergeben sich aus der Variation der invarianten Wirkung
(4) ergeben sich aus der Variation der invarianten Wirkung
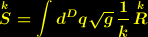 | (9) |
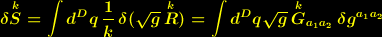 | (10) |
Im Variationsergebnis (10) für die Wirkung
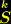 (9) tauchen keine Ableitungen dritter und vierter Ordnung des metrischen Tensors
(9) tauchen keine Ableitungen dritter und vierter Ordnung des metrischen Tensors 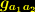 auf, weil sich bei der Ausführung der Variation alle Ableitungen dritter und vierter Ordnung des metrischen Tensors gegenseitig wegheben, so dass im Variationsergebnis keine Ableitungen höherer, als der zweiten Ordnung mehr auftauchen.
auf, weil sich bei der Ausführung der Variation alle Ableitungen dritter und vierter Ordnung des metrischen Tensors gegenseitig wegheben, so dass im Variationsergebnis keine Ableitungen höherer, als der zweiten Ordnung mehr auftauchen. , aus Dimensionsbereichen, die unabhängig voneinander und orthogonal zueinander existierende abgeschlossene Systeme darstellen.
Diese abgeschlossenen Systeme werden hier Dimensionszellen genannt, die dadurch charakterisiert sind, dass die jeweils in einer Dimensionszelle wirkenden Felder, keine Wirkung auf Dimensionsbereiche außerhalb von dieser Dimensionszelle haben können. Zwischen verschiedenen Dimensionszellen besteht also keinerlei Wechselwirkung und der Wirkungsbereich der Felder in einer Dimensionszelle ist nur auf diese Dimensionszelle selbst beschränkt. Um dies zu erreichen werden hier divergenzfreie Tensoren eingeführt, die sich jeweils aus einer Variation herleiten lassen, so dass sich damit Feldgleichungen konstruieren lassen, die divergenzfrei sind, und somit Erhaltungsgrößen darstellen.
, aus Dimensionsbereichen, die unabhängig voneinander und orthogonal zueinander existierende abgeschlossene Systeme darstellen.
Diese abgeschlossenen Systeme werden hier Dimensionszellen genannt, die dadurch charakterisiert sind, dass die jeweils in einer Dimensionszelle wirkenden Felder, keine Wirkung auf Dimensionsbereiche außerhalb von dieser Dimensionszelle haben können. Zwischen verschiedenen Dimensionszellen besteht also keinerlei Wechselwirkung und der Wirkungsbereich der Felder in einer Dimensionszelle ist nur auf diese Dimensionszelle selbst beschränkt. Um dies zu erreichen werden hier divergenzfreie Tensoren eingeführt, die sich jeweils aus einer Variation herleiten lassen, so dass sich damit Feldgleichungen konstruieren lassen, die divergenzfrei sind, und somit Erhaltungsgrößen darstellen.
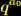 eine Koordinate, dann bezeichnet
eine Koordinate, dann bezeichnet 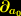 die einfache Ableitung, und
die einfache Ableitung, und 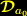 die kovariante Ableitung nach dieser Koordinate. Für
die kovariante Ableitung nach dieser Koordinate. Für 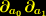 schreiben wir
schreiben wir 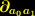 .]
.]
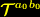 ist
ist 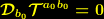 :
:
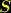 mit irgendwelchen Konstanten
mit irgendwelchen Konstanten 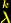 schreiben als:
schreiben als:
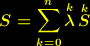
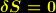 erhalten wir daraus eine relativistische Feldgleichung der Gravitation:
erhalten wir daraus eine relativistische Feldgleichung der Gravitation:
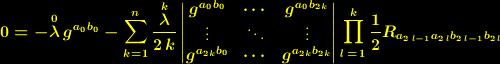
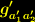 und
und 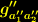 , die jeweils nur von den Koordinaten und Indizes des eigenen Dimensionsbereichs abhängen, so dass wir den metrischen Tensor
, die jeweils nur von den Koordinaten und Indizes des eigenen Dimensionsbereichs abhängen, so dass wir den metrischen Tensor 
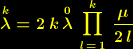
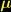 eine Konstante ist. Setzen wir für die Konstanten
eine Konstante ist. Setzen wir für die Konstanten 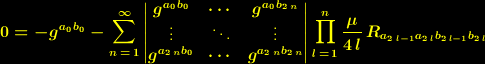
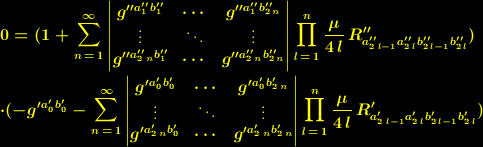
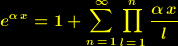
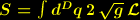 , mit
, mit
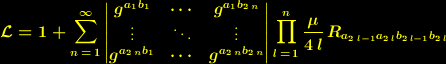
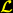 die selbe Gestalt hat, wie der Skalar, der sich durch die Vielweltenzerlegung dieser vielweltentauglichen Feldgleichung abseparieren lässt. Dieser Skalar hat den Charakter einer Exponentialfunktion, so dass er sich durch die Vielweltenzerlegung zu einem Produkt aus Skalaren der selben Gestalt zerlegen lässt, von denen jeder Skalar jeweils dem Dimensionsbereich einer Dimensionszelle zugeordnet ist.
Da sich auch das invariante Volumenelement
die selbe Gestalt hat, wie der Skalar, der sich durch die Vielweltenzerlegung dieser vielweltentauglichen Feldgleichung abseparieren lässt. Dieser Skalar hat den Charakter einer Exponentialfunktion, so dass er sich durch die Vielweltenzerlegung zu einem Produkt aus Skalaren der selben Gestalt zerlegen lässt, von denen jeder Skalar jeweils dem Dimensionsbereich einer Dimensionszelle zugeordnet ist.
Da sich auch das invariante Volumenelement